演示
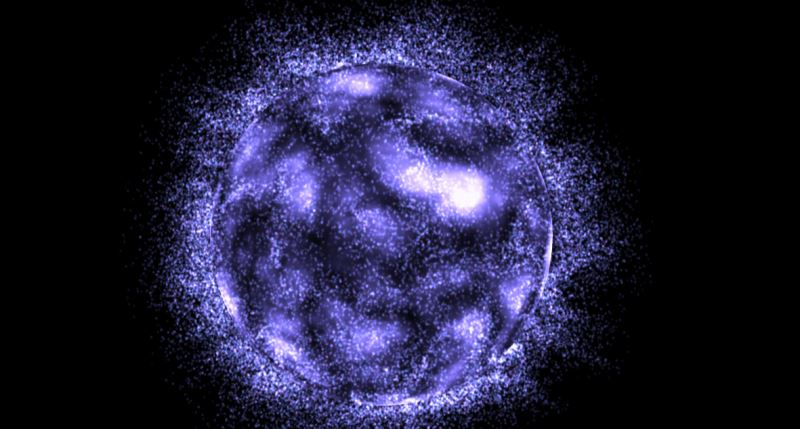
用过小米手机的应该见过这个动画

它这个球体会随着垃圾的清理被例子画分解 随着这个思路我们给他改造一下实现这种效果
技术栈
首先我们使用了一些好用的js脚本来帮助我们做这件事情

- EffectComposer和three来完成我们的渲染任务。在该对象上可以添加后期处理通道,使用它来渲染场景、应用通道和输出结果。
- 轨道控制器OrbitControls.js是一个相当神奇的控件,用它可以实现场景用鼠标交互,让场景动起来,控制场景的旋转、平移,缩放。等功能
- stats大家应该都用过吧。用来事件监听的。
源码
我们介绍一下部分内容:
首先建立画布
<canvas id="canvas"></canvas>
设置粒子的颜色:
<script type="x-shader/x-fragment" id="sphere-frag">
#define TAU 6.283185307179586
uniform float u_time;
varying float v_noise;
void main() {
vec3 color = vec3(0.);
vec3 q = 1. - vec3(
.9 * v_noise,
.4 * v_noise,
.3 * v_noise
);
color = mix(q,
vec3(.2, .3, .1),
clamp(pow(v_noise, 2.) * 4., 0., 1.));
color = mix(color,
vec3(.512, .461, .999),
clamp(length(q), 0., 1.));
color *= (pow(v_noise, 3.) .6 * pow(v_noise, 2.) .5 * v_noise);
gl_FragColor = vec4(color, 1.);
}
</script>对例子扩散的处理:
说实话这块比较复杂我是参考了一些大佬的处理方法。确实感觉到自己和大佬之间的差距了。
float cnoise(vec4 P) {
vec4 Pi0 = floor(P); // Integer part for indexing
vec4 Pi1 = Pi0 1.0; // Integer part 1
Pi0 = mod289(Pi0);
Pi1 = mod289(Pi1);
vec4 Pf0 = fract(P); // Fractional part for interpolation
vec4 Pf1 = Pf0 - 1.0; // Fractional part - 1.0
vec4 ix = vec4(Pi0.x, Pi1.x, Pi0.x, Pi1.x);
vec4 iy = vec4(Pi0.yy, Pi1.yy);
vec4 iz0 = vec4(Pi0.zzzz);
vec4 iz1 = vec4(Pi1.zzzz);
vec4 iw0 = vec4(Pi0.wwww);
vec4 iw1 = vec4(Pi1.wwww);
vec4 ixy = permute(permute(ix) iy);
vec4 ixy0 = permute(ixy iz0);
vec4 ixy1 = permute(ixy iz1);
vec4 ixy00 = permute(ixy0 iw0);
vec4 ixy01 = permute(ixy0 iw1);
vec4 ixy10 = permute(ixy1 iw0);
vec4 ixy11 = permute(ixy1 iw1);
vec4 gx00 = ixy00 * (1.0 / 7.0);
vec4 gy00 = floor(gx00) * (1.0 / 7.0);
vec4 gz00 = floor(gy00) * (1.0 / 6.0);
gx00 = fract(gx00) - 0.5;
gy00 = fract(gy00) - 0.5;
gz00 = fract(gz00) - 0.5;
vec4 gw00 = vec4(0.75) - abs(gx00) - abs(gy00) - abs(gz00);
vec4 sw00 = step(gw00, vec4(0.0));
gx00 -= sw00 * (step(0.0, gx00) - 0.5);
gy00 -= sw00 * (step(0.0, gy00) - 0.5);
vec4 gx01 = ixy01 * (1.0 / 7.0);
vec4 gy01 = floor(gx01) * (1.0 / 7.0);
vec4 gz01 = floor(gy01) * (1.0 / 6.0);
gx01 = fract(gx01) - 0.5;
gy01 = fract(gy01) - 0.5;
gz01 = fract(gz01) - 0.5;
vec4 gw01 = vec4(0.75) - abs(gx01) - abs(gy01) - abs(gz01);
vec4 sw01 = step(gw01, vec4(0.0));
gx01 -= sw01 * (step(0.0, gx01) - 0.5);
gy01 -= sw01 * (step(0.0, gy01) - 0.5);
vec4 gx10 = ixy10 * (1.0 / 7.0);
vec4 gy10 = floor(gx10) * (1.0 / 7.0);
vec4 gz10 = floor(gy10) * (1.0 / 6.0);
gx10 = fract(gx10) - 0.5;
gy10 = fract(gy10) - 0.5;
gz10 = fract(gz10) - 0.5;
vec4 gw10 = vec4(0.75) - abs(gx10) - abs(gy10) - abs(gz10);
vec4 sw10 = step(gw10, vec4(0.0));
gx10 -= sw10 * (step(0.0, gx10) - 0.5);
gy10 -= sw10 * (step(0.0, gy10) - 0.5);
vec4 gx11 = ixy11 * (1.0 / 7.0);
vec4 gy11 = floor(gx11) * (1.0 / 7.0);
vec4 gz11 = floor(gy11) * (1.0 / 6.0);
gx11 = fract(gx11) - 0.5;
gy11 = fract(gy11) - 0.5;
gz11 = fract(gz11) - 0.5;
vec4 gw11 = vec4(0.75) - abs(gx11) - abs(gy11) - abs(gz11);
vec4 sw11 = step(gw11, vec4(0.0));
gx11 -= sw11 * (step(0.0, gx11) - 0.5);
gy11 -= sw11 * (step(0.0, gy11) - 0.5);
vec4 g0000 = vec4(gx00.x,gy00.x,gz00.x,gw00.x);
vec4 g1000 = vec4(gx00.y,gy00.y,gz00.y,gw00.y);
vec4 g0100 = vec4(gx00.z,gy00.z,gz00.z,gw00.z);
vec4 g1100 = vec4(gx00.w,gy00.w,gz00.w,gw00.w);
vec4 g0010 = vec4(gx10.x,gy10.x,gz10.x,gw10.x);
vec4 g1010 = vec4(gx10.y,gy10.y,gz10.y,gw10.y);
vec4 g0110 = vec4(gx10.z,gy10.z,gz10.z,gw10.z);
vec4 g1110 = vec4(gx10.w,gy10.w,gz10.w,gw10.w);
vec4 g0001 = vec4(gx01.x,gy01.x,gz01.x,gw01.x);
vec4 g1001 = vec4(gx01.y,gy01.y,gz01.y,gw01.y);
vec4 g0101 = vec4(gx01.z,gy01.z,gz01.z,gw01.z);
vec4 g1101 = vec4(gx01.w,gy01.w,gz01.w,gw01.w);
vec4 g0011 = vec4(gx11.x,gy11.x,gz11.x,gw11.x);
vec4 g1011 = vec4(gx11.y,gy11.y,gz11.y,gw11.y);
vec4 g0111 = vec4(gx11.z,gy11.z,gz11.z,gw11.z);
vec4 g1111 = vec4(gx11.w,gy11.w,gz11.w,gw11.w);
vec4 norm00 = taylorInvSqrt(vec4(dot(g0000, g0000), dot(g0100, g0100), dot(g1000, g1000), dot(g1100, g1100)));
g0000 *= norm00.x;
g0100 *= norm00.y;
g1000 *= norm00.z;
g1100 *= norm00.w;
vec4 norm01 = taylorInvSqrt(vec4(dot(g0001, g0001), dot(g0101, g0101), dot(g1001, g1001), dot(g1101, g1101)));
g0001 *= norm01.x;
g0101 *= norm01.y;
g1001 *= norm01.z;
g1101 *= norm01.w;
vec4 norm10 = taylorInvSqrt(vec4(dot(g0010, g0010), dot(g0110, g0110), dot(g1010, g1010), dot(g1110, g1110)));
g0010 *= norm10.x;
g0110 *= norm10.y;
g1010 *= norm10.z;
g1110 *= norm10.w;
vec4 norm11 = taylorInvSqrt(vec4(dot(g0011, g0011), dot(g0111, g0111), dot(g1011, g1011), dot(g1111, g1111)));
g0011 *= norm11.x;
g0111 *= norm11.y;
g1011 *= norm11.z;
g1111 *= norm11.w;
float n0000 = dot(g0000, Pf0);
float n1000 = dot(g1000, vec4(Pf1.x, Pf0.yzw));
float n0100 = dot(g0100, vec4(Pf0.x, Pf1.y, Pf0.zw));
float n1100 = dot(g1100, vec4(Pf1.xy, Pf0.zw));
float n0010 = dot(g0010, vec4(Pf0.xy, Pf1.z, Pf0.w));
float n1010 = dot(g1010, vec4(Pf1.x, Pf0.y, Pf1.z, Pf0.w));
float n0110 = dot(g0110, vec4(Pf0.x, Pf1.yz, Pf0.w));
float n1110 = dot(g1110, vec4(Pf1.xyz, Pf0.w));
float n0001 = dot(g0001, vec4(Pf0.xyz, Pf1.w));
float n1001 = dot(g1001, vec4(Pf1.x, Pf0.yz, Pf1.w));
float n0101 = dot(g0101, vec4(Pf0.x, Pf1.y, Pf0.z, Pf1.w));
float n1101 = dot(g1101, vec4(Pf1.xy, Pf0.z, Pf1.w));
float n0011 = dot(g0011, vec4(Pf0.xy, Pf1.zw));
float n1011 = dot(g1011, vec4(Pf1.x, Pf0.y, Pf1.zw));
float n0111 = dot(g0111, vec4(Pf0.x, Pf1.yzw));
float n1111 = dot(g1111, Pf1);
vec4 fade_xyzw = fade(Pf0);
vec4 n_0w = mix(vec4(n0000, n1000, n0100, n1100), vec4(n0001, n1001, n0101, n1101), fade_xyzw.w);
vec4 n_1w = mix(vec4(n0010, n1010, n0110, n1110), vec4(n0011, n1011, n0111, n1111), fade_xyzw.w);
vec4 n_zw = mix(n_0w, n_1w, fade_xyzw.z);
vec2 n_yzw = mix(n_zw.xy, n_zw.zw, fade_xyzw.y);
float n_xyzw = mix(n_yzw.x, n_yzw.y, fade_xyzw.x);
return 2.2 * n_xyzw;
}到此这篇关于JavaScript仿小米实现球体分解动画的文章就介绍到这了,更多相关JavaScript球体分解动画内容请搜索Devmax以前的文章或继续浏览下面的相关文章希望大家以后多多支持Devmax!